Better Benchmarks Through Graphs

Isn't the ambiguity in the word *graphs* fun?

This is a blog post version of a talk I gave at the Northwest Database Society meeting last week. The slides are here, but I don’t believe the talk was recorded.

I believe that one of the things that’s holding back databases as an engineering discipline (and why so much remains stubbornly opinion-based) is a lack of good benchmarks, especially ones available at the design stage. The gold standard is designing for and benchmarking against real application workloads, but there are some significant challenges achieving this ideal. One challenge¹ is that, as in any system with concurrency, traces capture the behavior of the application running on another system, and they might have issued different operations in a different order running on this one (for example, think about how in most traces it’s hard to tell the difference between application thinking and application waiting for data, which could heavily influence results if we’re trying to understand the effect of speeding up the waiting for data portion). Running real applications is better, but is costly and raises questions of access (not all customers, rightfully, are comfortable handing their applications over to their DB vendor).

Industry-standard benchmarks like TPC-C, TPC-E, and YCSB exist. They’re widely used, because they’re easy to run, repeatable, and form a common vocabulary for comparing the performance of systems. On the other hand, these benchmarks are known to be poorly representative of real-world workloads. For the purposes of this post, mostly that’s because they’re too easy. We’ll get to what that means later. First, here’s why it matters.

Designing, optimizing, or improving a database system requires a lot of choices and trade-offs. Some of these are big (optimistic vs pessimistic, distributed vs single machine, multi-writer vs single-writer, optimizing for reads or writes, etc), but there are also thousands of small ones (“how much time should I spend optimizing this critical section?”). We want benchmarks that will shine light on these decisions, allowing us to make them in a quantitative way.

Let’s focus on just a few of the decisions the database system engineer makes: how to implement atomicity, isolation, and durability in a distributed database. Three of the factors that matter there are transaction size (how many rows?), locality (is the same data accessed together all the time?), and coordination (how many machines need to make a decision together?). Just across these three factors, the design that’s best can vary widely.

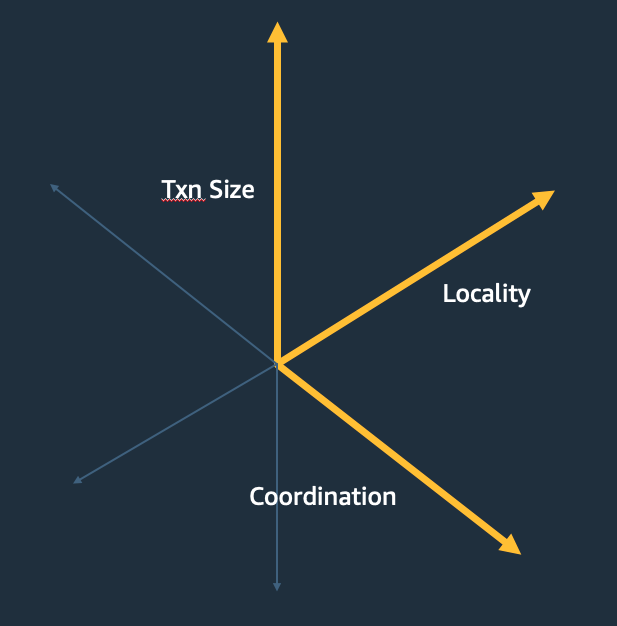
If we think of these three factors as ones that define a space². At each point in this space, keeping other concerns constant, some design is best. Our next challenge is generating synthetic workloads—fake applications—for each point of the space. Standard approaches to benchmarking sample this space sparsely, and the industry-standard ones do it extremely poorly. In the search for a better way, we can turn, as computer scientist so often do, to graphs.

In this graph, each row (or other object) in our database is a node, and the edges mean transacted with. So two nodes are connected by a (potentially weighted) edge if they appear together in a transaction. We can then generate example transactions by taking a random walk through this graph of whatever length we need to get transactions of the right size.

The graph model seems abstract, but is immediately useful in allowing us to think about why some of the standard benchmarks are so easy. Here’s the graph of write-write edges for TPC-C neworder (with one warehouse), for example.

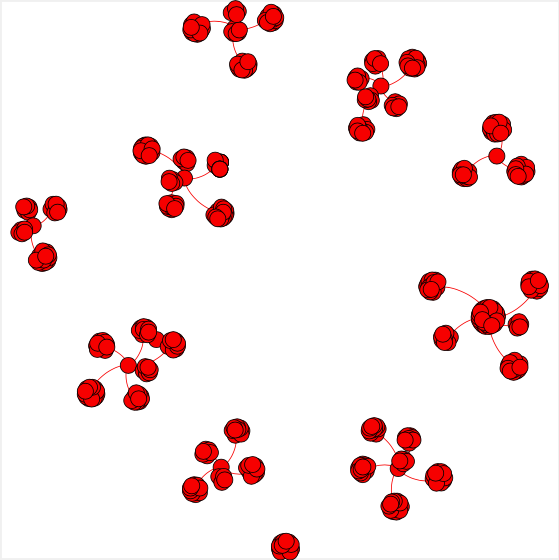
Notice how it has 10 disjoint islands. One thing that allows us to see is that we could immediately partition this workload into 10 shards, without ever having to execute a distributed protocol for atomicity or isolation. Immediately, that’s going to look flattering to a distributed database architecture. This graph-based way of thinking is generally a great way of thinking about the partitionability of workloads. Partitioning is trying to draw a line through that graph which cuts as few edges as possible³.

If we’re comfortable that graphs are a good way of modelling this problem, and random walks over those graphs⁴ are a good way to generate workloads with a particular shape, we can ask the next question: how do we generate graphs with the properties we want? Generating graphs with particular shapes is a classic problem, but one approach I’ve found particularly useful is based on the small-world networks model from Watts and Strogatz⁶. This model gives us a parameter $p$ which, which allows us to vary between ring lattices (the simplest graph with a particular constant degree), and completely random graphs. Over the range of $p$, long-range connections form across broad areas of the graph, which seem to correlate very well with the contention patterns we’re interested in exploring.

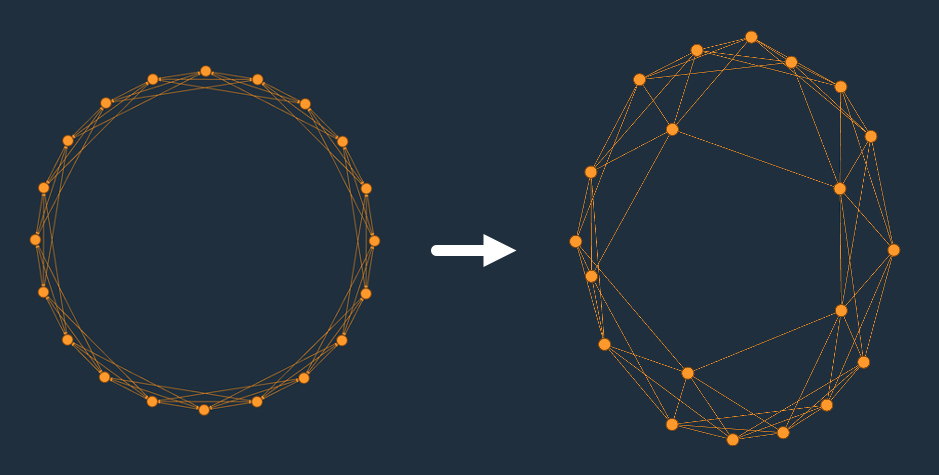
That gives us two of the parameters we’re interested in: transaction size is set by the length of random walks we do, and coordination which is set by adjusting $p$. We haven’t yet solved locality. In our experiments, locality is closely related to degree distribution, which the Watts-Strogatz model doesn’t control very well. We can easily control the central tendency of that distribution (by setting the initial degree of the ring lattice we started from), but can’t really simulate the outliers in the distribution that model things like hot keys.

In the procedure for creating these Watts-Strogatz graph, the targets of the rewirings from the ring lattice are chosen uniformly. We can make the degree distribution more extreme by choosing non-uniformly, such as with a Zipf distribution (even though Zipf seems to be a poor match for real-world distributions in many cases). This lets us create a Watt-Strogatz-Zipf model.

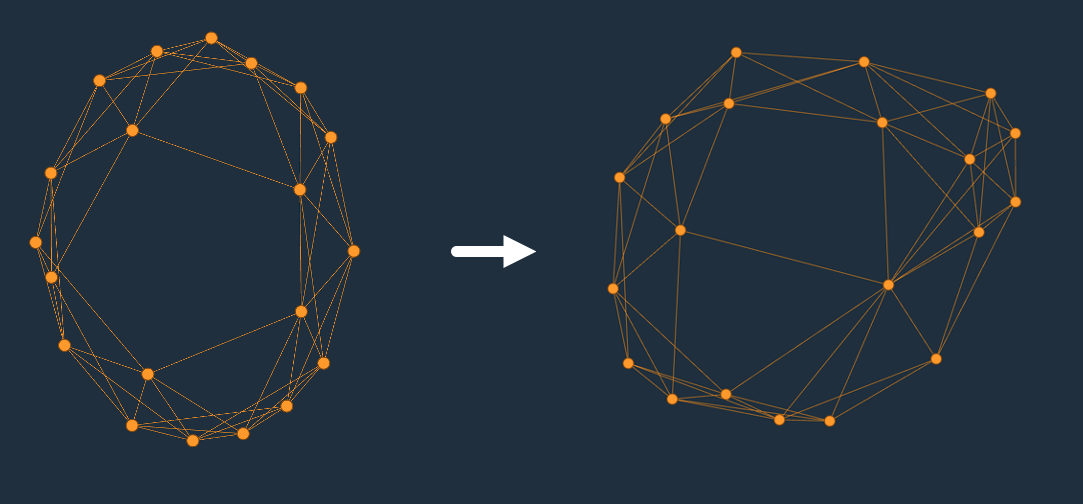
Notice how we have introduced a hot key (near the bottom right). Even if we start our random walk uniformly, we’re quite likely to end up there. This kind of internal hot key is fairly common in relational transactional workloads (for example, secondary indexes with low cardinality, or dense auto-increment keys).

This approach to generating benchmark loads has turned out to be very useful. I like how flexible it is, how we can generate workloads with nearly any characteristics, and how well it maps to other graph-based ways of thinking about databases. I don’t love how the relationship between the parameters and the output characteristics is non-linear in a potentially surprising way. Overall, this post and talk were just scratching the surface of a deep topic, and there’s a lot more we could talk about.

Play With the Watts-Strogatz-Zipf Model

Footnotes

1. There’s an excellent discussion of more problems with traces in Traeger et al’s A Nine Year Study of File System and Storage Benchmarking.
2. I’ve drawn them here as orthogonal, which they aren’t in reality. Let’s hand-wave our way past that.
3. This general way of thinking dates back to at least 1992’s On the performance of object clustering techniques by Tsangaris et al (this paper’s Expansion Factor, from section 2.1, is a nice way of thinking about distributed databases scalability in general). Thanks to Joe Hellerstein for pointing this paper out to me. More recently, papers like Schism and Chiller have made use of it.
4. There’s a lot to be said about the relationship between the shape of graphs and the properties of random walks over those graphs. Most of it would need to be said by somebody more competent in this area of mathematics than I am.
5. The degree distribution of these small-world networks is a whole deep topic of its own. Roughly, there’s a big spike at the degree of the original ring lattice, and the distribution decays exponentially away from that (with the exponent related to $p$).
6. Google Scholar lists nearly 54000 citations for this paper, so its not exactly obscure.

Other Posts

• 25 Apr 2024 » MemoryDB: Speed, Durability, and Composition.
• 17 Apr 2024 » Formal Methods: Just Good Engineering Practice?
• 25 Mar 2024 » Finding Needles in a Haystack with Best-of-K